前言
关于对极几何,从去年最开始接触视觉SLAM的时候就经常看到,那时候还以为它是一门几何学科,觉得要了解一门新的学科范围太大,于是就鸽了没有去看。最近开始研究立体视觉,这次是躲是不过了,开始学习吧。查过一通资料才恍然大悟,原来这东西哪是是什么新学科,只是一种特定情况下的几何模型而已,所以这些专有名词就是喜欢吓唬人。
不过话虽然是这样说,但是我丝毫也没有看轻它的意思,在多角度视觉成像的分析中,对极几何其研究基础。
对极几何是什么?
在我查找的资料中,我觉得比较好的解释是:对极几何是相机在两个不同的位置生成的两幅图像,其拍摄位置和生成图像之间的特殊几何关系。其基本几何模型如下图所示:
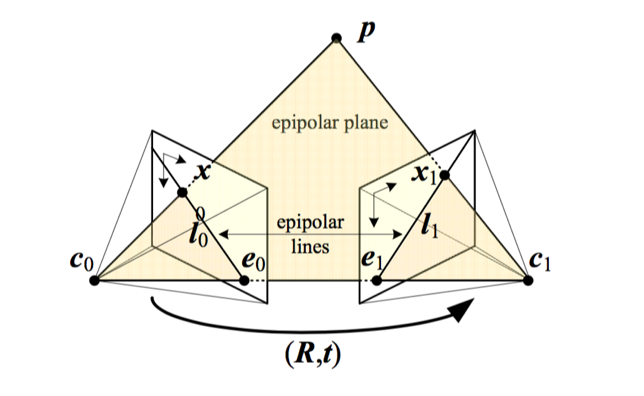
对极几何有什么用?
在介绍对几何详细概念前,我想先说一下它有什么用,这是我在写这这篇文章的时候一直在想的问题,从单纯的概念解释并不是那么直接就理解到它的应用场景,那对极几何有什么用呢?
其一就是立体匹配问题,对于已知两视角空间位置关系的情况下,由于对极几何这个几何模型限定的约束条件,使得在立体图像对上搜索空间上的分别在两个图像中的位置只需要相应的对极线上找,把原来的二维搜搜问题,直接简化为一维搜索,双目测距就是这方面得应用之一。
其二就是确定两个拍摄点相对位置与姿态问题,在未知视角位置的情况下,通过搜索图像对中的匹配点,可以求得两个位置和姿态得相对关系,这一点常用在机器人导航、地图得生成、三维重建等方面。
基本概念
- 极点(Epipoles):两个相机得基线与两个成像平面得交点,如上图中的e0、e1
- 极线(Epipolar Lines):空间中点在成像平面上的投影点与极点的连线,如上图中的l0、l1
- 极平面(Epipolar Plane):空间中的点与两个相机的光轴中心点所组成的平面,如上图c0、c1、p所在的面
对极约束、基础矩阵和本质矩阵
对于对极几何,通过上图的几何模型,我们能得到不少有用的结论,但是去除那些细枝末节的东西,其实只有对极约束这个性质才是描叙对极几何最本质特点的性质。
对极约束
如下图所示,假定相机参数已知,那么对于空间中P点,它将和两个相机的中心点O1和O2,唯一确定对极几何的几何关系,极点、极线、极平面都将确定,而对极约束描叙的就是:在平面1上成像为p的所有空间点,其必定投影在平面2的极线上,反之亦然。
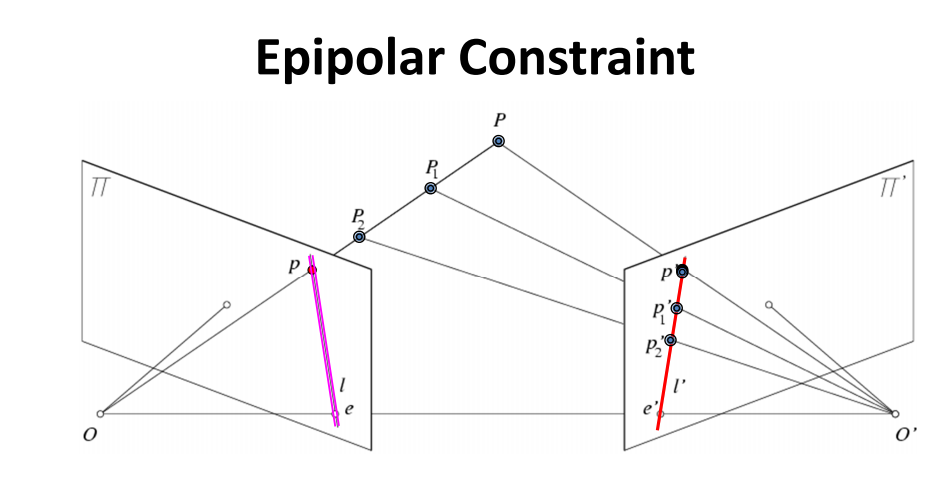
在实际应用中,我们可以直接使用这条性质,但是却不是那么的直接,所以在数学上我们引入的基础矩阵和本质矩阵,用一个非常简洁的等式就概括这样一个关系。我发现有一个很有意思的现象:往往数学的描叙是不直接、更难理解的,但是在这里我反倒觉得使用了基础矩阵或本质矩阵的等式是更直接、更清晰的。
基础矩阵和本质矩阵
为了表示对极约束中在两个成像平面上的点的相对关系,在数学上我们只需要加入一个矩阵(本质矩阵或者基础矩阵)就可以简洁的写出两者的等式关系。
对于本质矩阵E其矩阵等式为:
$pl^T E pr = 0$
对于基础矩阵F其矩阵等式为:
$cl^T F cr = 0$
其中pl和cl表示空间中的点投影在左视图的位置,pr和cr为其投影在右视图中的位置,p和c表示视图中的点在不同坐标下的表示。根据上面的任意一个等式,当我们已知空间中一点在左右视图中的两个位置坐标和基础矩阵(或本质矩阵)这三个中的两者,我们就能够计算得到第三个未知量(对于求E和F来说,可能需要多个点联立求解,因为这两个矩阵中的未知量比较多)。
本质矩阵(Essential Matrix)
上面两式,我们可以看到其等式形式是一模一样的,唯一的区别就在于,两种是在不同坐标系中的表达。本质矩阵E连接的是不同视角下摄像机坐标系下两个投影点的关系,所以pl和pr是在摄像机坐标系下的坐标。
假定两个投影平面的坐标系转化为:旋转R和平移T,那么本质矩阵E与R和T由如下关系(公式推导就省略了):
$ E = [T_x] \cdot R$
其中(向量叉乘转矩阵的方法):
$ [T_x] \cdot R = T \times R$
基础矩阵(Fundamental Matrix)
基础矩阵F链接的是在图像坐标系下两个视图图像中的坐标像素坐标的关系,所以cl和cr是图像的像素坐标。我们知道从摄像机坐标系到图像的像素坐标系,是由摄像机的内参矩阵K来确定的,因此基础矩阵与旋转矩阵R和平移向量T之间的关系还需要有摄像机的内参矩阵加入:
$ F = Kl^{-T} \cdot [T_x] \cdot R \cdot Kr^{-1}$
显然其与本质矩阵的关系如下:
$ F = Kl^{-T} \cdot E \cdot Kr^{-1}$