前言
前面我总结过梯度下降以及基于梯度下降的几种主要的优化方法,但是那是仅仅局限于深度学习领域的,而现在我希望将眼光扩大到整个数值优化领域。作为初学者,古老的牛顿法是我们很好的入门起点。
牛顿法的简介
牛顿法(Newton’s method)是由大名鼎鼎的牛顿于1671提出1736公开的的《流数法》一书中提出的方法,他是一种在实数和复数域近似求解方程的方法。这句话多数百科上的简介,基本上看不懂,结合应用场景,我觉得牛顿法可以描叙成:为了求函数的最值,使用函数的二阶泰勒展开,利用函数的一阶导数等于0推导的迭代方法。也许描叙得并不准确,但是我觉得这样的表述至少前面要具体和清晰不少。
假定有函数f(x),我们需要求其极值点,则牛顿法的迭代公式如下:
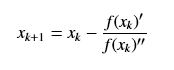
切线法解释
牛顿法常常又被称为切线法,这是因为求原始函数f(x)得极值点,等同于求其导数等于0的解,那么画出其导数曲线,从初始点画切线,将切线于x轴的交点值作为下一次x值,它将不断的接近曲线于x轴的交点,也就是f(x)的导数为0的地方。当我们从切线得角度取理解牛顿法就就现得非常非常的简单,其迭代动图如下所示:
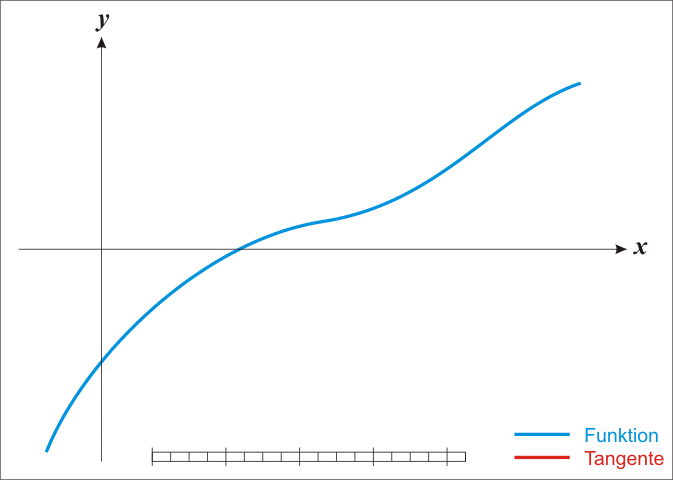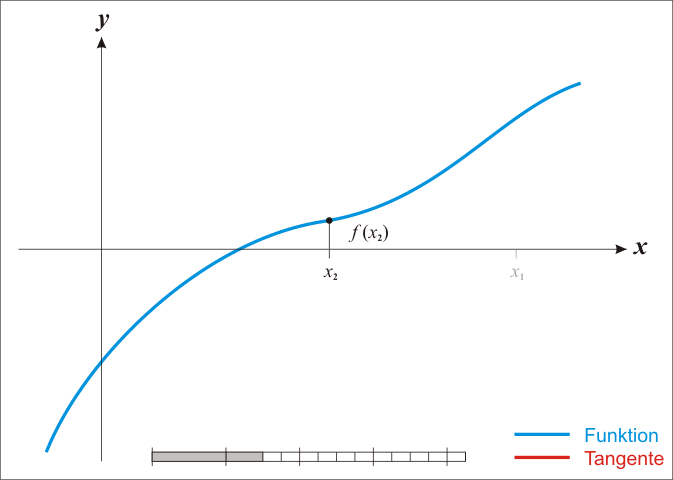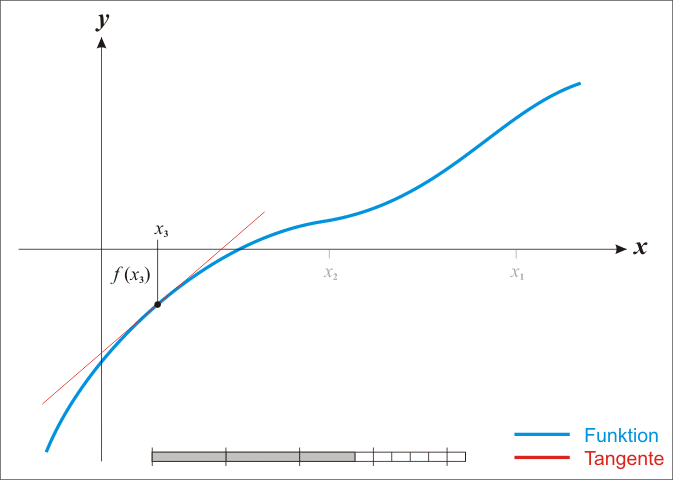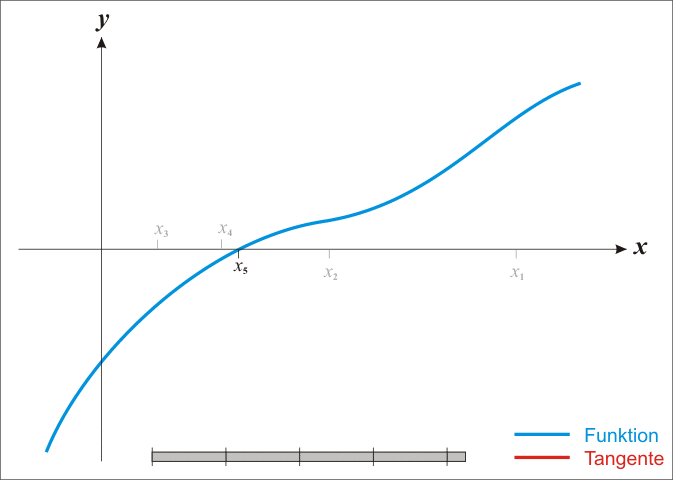
当然除了直观的理解,还需要更严谨的数学推导,使用切线法得到上面牛顿法的迭代式也是很简单的。取初值点(x0,f(x0)),假定f(x)的导数为g(x),则上图中的曲线就不是f(x)了,而是g(x),以x0做g(x)的切线,则切线的直线方程为:
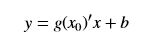
由于切线过(x0, g(x0))点,因此:
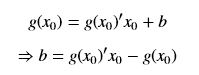
切线于x轴的交点x1作为下一个迭代点,根据上面的直线方程有:
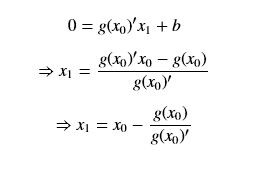
写成通项的形式,并重新带入f(x)就成了:
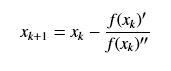
二阶泰勒展开的推导
使用二阶泰勒展开在解释上没有上面切线法直观,但是从数学的看是更加严谨的。设xk为当前最小值点的估计值,首先对f(x)进行在xk附近的泰勒展开,对其做近似,保留常数项、一阶项和二阶项,舍弃后面的高阶项:
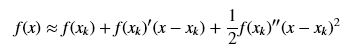
将近似项用h(x)来表示,则:
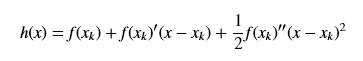
我们利用求h(x)的极值来近似得到f(x)的极值,h(x)的极值点,则其一阶导数为0,我对h(x)求导(注意是对x求导,x_k是常数),得到:
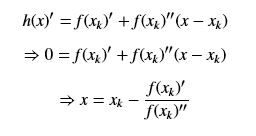
写成递推形式为:
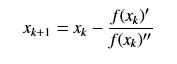
优缺点
从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快,但是正是由于它要求二阶导数,在多维的情况下,就是需要求海森(Hessian)矩阵的逆矩阵,计算比较复杂。