前言
深度学习的优化算法基本上都是基于梯度下降的,不过在复杂的网络训练中,仅仅使用梯度下降是远远不够的。一方面是由于深度学习的数据量巨大,不可能将数据全部带入求梯度下降;另一方面是深度的学习的待优化的参数太巨大,这么多参数组成了超高的维度必然在各个维度上的尺度非常的不一致,造成优化困难。所以在实际中,一般都是使用中的方法都是改进过的优化算法,本文主要介绍一下集中优化算法:
- SGD
- Momentum
- RMSprop
- Adam
各种优化算法的关系
其实除了以上几种外,还有很多其他的相关优化算法,这对于深度学习初学者来说,简直就是噩梦,感觉还没开始进入正题就陷入深渊。不过虽然优化算法本身是一个水很深的一大研究方向,但是针对深度学习的优化算法其实还是相对狭窄很多。正如上面所提到的那样,深度学习的优化算法本质上都是基于梯度下降的,所以一旦我们找倒了他们之间彼此的联系,再来理解就要简单许多。
首先我们先来看看基本的梯度下降的公式:
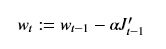
使用当前点的梯度与学习率来更新当前的参数大小,其中梯度主要指引优化的方向,学习率控制更新的步长。
再此基础上,SGD是为了解决数据量大,无法使用全部数据用来更新梯度;Momentum则是为了解决SGD由于数据批次的差异导致的梯度震荡优化速度慢的问题,RMSprop则是从学习率的角度出发提出自适应学习率的方法,而Adam则完全就是Momentum和RMSprop的方法的结合作用。RMSprop和Adam是根据实际情况自适应学习率,所以它们实际的学习率是动态调整的。
SGD
SGD是Stochastic Gradient Descent的缩写,SGD在基本的梯度下降方法做的改进就是,仅仅使用一个样本对梯度进行更新。这样做的好处就是每一个数据都是会独立作用到梯度更新上,比起使用全部数据才更新一次梯度的方法数据利用效率要高很多。但是由于数据的随机性、以及噪声的干扰,使得SGD每次更新的梯度对数据整体而言可能并不是下降的方向,虽然训练速度较快,但是震荡厉害、准确度下降。
为了减小SGD的震荡,使收敛更稳定,我可以使用去一个折中的方案:每次使用一小批数据(mini batch)来更新梯度,这样既提供了数据的利用率,又可以增加数据的稳定性,这种被称为Mini-Batch Gradient Descent(MBGD)。
不过在一些深度学习框架的实际使用中,这里有个问题我发现一般都只有SGD而没有MBGD,但是在训练时又分了mini batch。这就很奇怪了,明明只有MBGD才会使用到mini batch。我个人认为这是由于,神经网络计算数据的计算都是向量、矩阵化的,我们一般称为tensor,所以即使有多个数据,一般都是组成一个tensor作为一个数据输入到网络中的,而且网络也只会经过一次计算,所以形式上与SGD时一致的,但是效果却是MBGD一样。
指数滑动平均EMA
在说明后面的优化算法前,需要先了解指数滑动平均EMA,因为不管是Monentum还是RMSprop都是利用EMA对优化过程进行平滑的。EMA全称是Exponential Moving Average,是一种使用非常广泛的平滑方法,如股票、气温变化曲线,它能够用历史数据对当前数据进行平滑,以保持曲线整体的稳定性。
V表示平滑结果,theta 表示当前数据值,beta表示平滑系数,则EMA的计算方法如下:
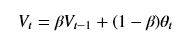
如果使用上面的迭代关系,从V0开始算,则Vt的可以得到公式如下:
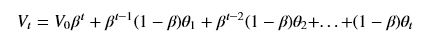
可以看到Vt使用到了所有历史数据,越靠近的数据影响越大,且越往后其影响力呈指数下降。
下图是使用EMA平滑气温变化曲线效果(蓝色点为原始数据,红、黄、绿色的曲线为使用了不同的平滑系数的EMA的效果):
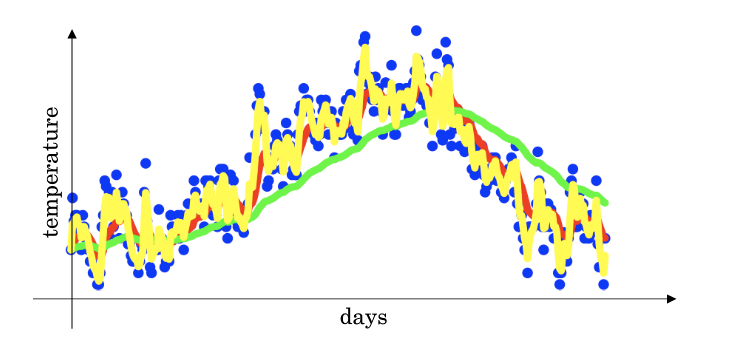
EMA的偏差修正
在使用EMA平滑数据时候,需要注意在最开始的时候,由于历史数据很少或者没有,而我们设置V0初值却占了绝对主要的影响。一般V0会设置为0,这样会导致平滑曲线与实际数据相差甚远,不过随着历史数据越来越多,这个偏差就会变得越来越小。为了修正最开始的时候出现的偏差,我们一般可以使用如下公式对结果进行修正:
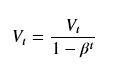
当V0 = 0时,当很小的时候将原始数据的影响放大,后面随着t的变大,修正的影响变小。
Momentum
前面说过SGD由于即使加入了mini batch后,仍然由于数据的随机性,所以当前所mini batch的数据与整个数据的分布可能不一致,导致SGD在收敛时震荡厉害。Monmentum为了减小震荡,使用了EMA来平滑梯度,从而达到当前参数优化不仅取决于当前步的梯度,还取决于历史梯度值。
Momentum方法将梯度下降比拟为一个滚动下山的小球,小球每一时刻的运动状态不仅取决与其当前所受合力的作用,还取决于其原来的运动状态。Momentun借用了物理学中动量的概念,用动量代替梯度作为参数更新的动力,动量的计算实际上就使用EMA的方法求得的:
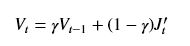
可以理解为J的导数为当前合力作用与当前运动状态Vt共同决定下一刻的运动状态,一般超参数gramma设置为0.9,参数更新公式将变为:
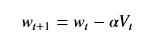
Momentum方法通过使用EMA平滑了原始梯度数据,让训练时收敛更稳定。
RMSprop
相比Momentum使用历史数据来保持稳定,RMSprop则是直接考虑不同维度上的梯度变化的大小,在相同学习率下,某个维度梯度变化大,则在参数更新的时候步长方向都会较大,RMSprop算法不希望这些在不同维度上参数更新差异太大,因此它引入一个衰减因子来平衡不同维度上的差异。直观的理解,SGD的出现震荡,很大的原因就是由于其在某个维度上更新速度慢,而在另外的维度上更新速度快导致来回摆动。
另外使用梯度的平方作为抑制因子,平且通过EMA方法进行指数加权来平滑抑制因子,更新方程如下:
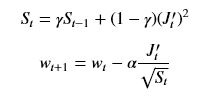
Adam
Adam是Adaptive Moment Estimation的缩写,前面提过Adam是Momentum与RMSprop的结合,它综合了上面两个算法的特点,既使用动量的方法平滑了更新的路径,又使用了衰减因子平衡了不同维度上的更新尺度。不过需要注意的一点是,Adam在用EMA做平滑的时候使用了偏差矫正,计算公式如下:
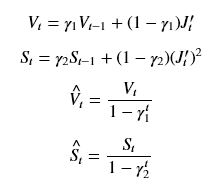
最后的参数更新规则为: