介绍
反向传播，即Backpropagation（BP）是the backward propagation of errors的缩写，顾名思义就是误差向后传播（输入/激励前向传播）。反向传播算法对深度学习的发展具有极其重要的意义，可以说是当前深度学习领域中最为核心的一个算法了，它的存在让我们训练更深的深度神经网络变得简单易行。
反向传播算法使用在如梯度下降的优化算法中，作为其计算个网络层中参数的梯度的方法来使用，其主要解决的问题是网络中各层权重参数对最终的损失函数（真实值与预测值的偏差）的贡献量。本文假定我们都是知道像梯度下降这类优化方法的，而梯度下降需要使用梯度值，所以在本文中我们的目标是如何求权重梯度。
反向传播算法利用最基本的链式求导法则来推导计算公式，本身是比较基础的知识，但是一旦结合上多层结构的神经网络就变得繁琐了，特别是对于初学者，各种上下标和字母标记让人看得云里雾里。所以当我开始理解反向传播算法的时候不妨抛开网络本身，先理解其计算方法的本质，然后再结合网络结构推导。当然前提是对神经网络本身的各个基本网络连接与作用有相当的了解。
链式求导法则
梯度是各个自变量对因变量的偏导的集合，所以求梯度的问题等价于求各个分量的偏导。那么怎么求偏导呢？除了那些最基本函数的导数公式外，对复合函数求导的链式法则肯定是必须的，而这些如 f(g(t(x))) 的形式不正是深度学习中神经网络一层一层的形式么。
我将链式求导法则的基本的公式列出，以帮助回忆其内容，这些都是高等数学微积分课程的基础知识，我就不详细说明了。
对于F(g(x))有（直接贴wiki上的公式）：
另一种写法可能更容易理解，对于z=f(y)、y=g(x)有：
如上所说，当前深度学习的神经网络是层级式的，每一层的结构都可以看成其输出对其输入的函数，而上一层的输入到一层输入的连接也可以同样看成一个函数，如此神经网络的整体结构就可以看作一层一层函数的嵌套。当我需要求得某一层参数得导数时，就可以直接使用链式法则即可，这就反向传播算法得数学基础，很简单吧。
用计算图表示网络
我们以两层网络为例，为了简化流程，我们先隐藏细节，使用计算图来表示神经网络的结构，如下图所示：
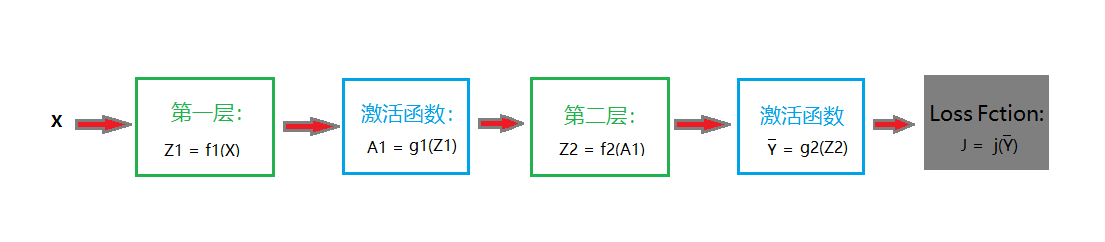
如上我们有两层神经网络的结构，输入X，经过两层网络连接和激活函数输出Yhat，通过损失函数j来衡量真实值与估计值之前的误差大小，误差的结果就是J。输入的数据X通过网络向前传播，而误差J则从输出端通过网络逐层反向传播，这就是反向传播算法的直观描叙。
另外上图中的数值结果表示我都用大写字母写，用以表示这是一个向量或者矩阵。(博客显示公式不是很好，只能截图了)
- 数据正向传播：
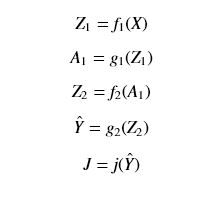
- 求导反向求（应用链式求导法则）：
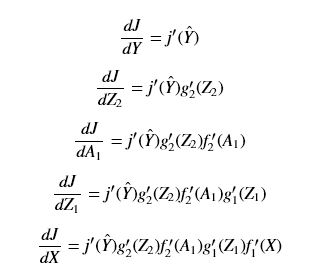
上面公式就是使用链式求导法则得到各层输入对最终损失函数的导数，不过在使用中我们真正需要的是：网络层中各层的权重W和偏置B对损失函数的偏导（注意激活函数是没
有W和B的），所以有如下等式：
- 第二层网络：
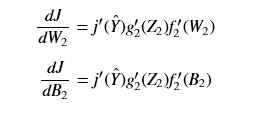
- 第一层网络：
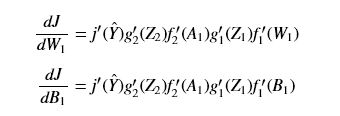
从上面这些公式可以看到，W和B的偏导是从输出端的偏导开始求起，然后逐层求到输入端的。
全连接神经网络的形式
以上面的计算图为基础，我们开始分析特定的网络，以常见的全连接神经网络多分类器为例子，简单示意图如下（只是示意图，不是说明其中每层中神经元的个数就是图中所示）：
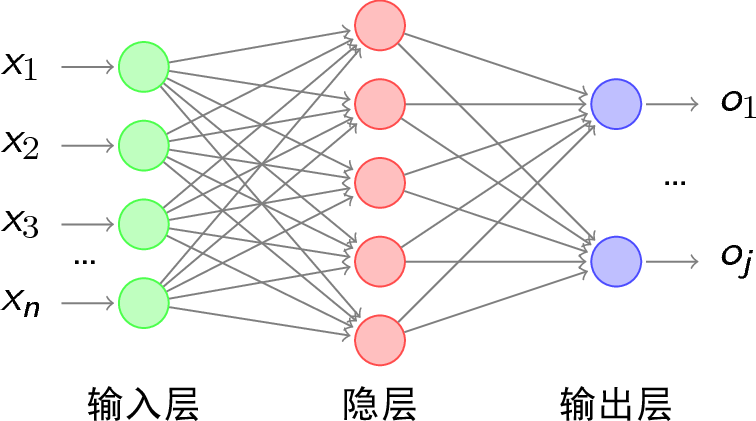
那么我们可以写出有一个隐含层（即总共两层）多分类网络的各个表达式：
- 交叉熵损失函数j为，假定有n个类别，注意这里的求和是对后面向量中的元素求和，结果是一个标量：
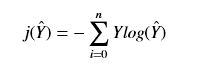
- 第二层的激活函数都使用softmax函数，注意分母中的求和表示对向量Z2中的每一个元素求和（顺便写一下特殊化的二分类的sigmod函数）：
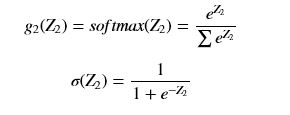
- 第一层激活函数使用relu函数：
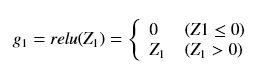
- 两层全连接层函数：
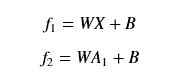
整合其前向传播的公式如下：
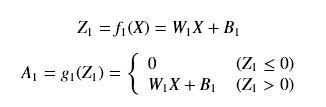
下面不写A1等于0的部分
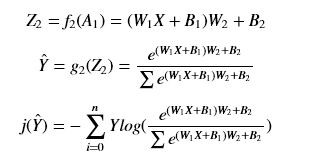
求这个全连接网络特定函数的导数
- 损失函数的导数：
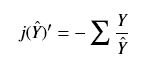
- sigmod函数的导数比较简单(先用通用型的x来作为自变量)：
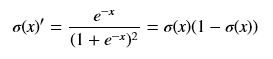
- softmax就会稍微复杂一些，虽然它仍然是输入一个向量，输出一个相同尺寸的向量，但是由于softmax函数分母是各项的求和，使得向量中的各个元素不再独立。所以求偏导时我们需要将向量拆分后讨论，用小写字母x和o加下标来表示向量中不同元素（x输入元素，o输出元素，i表示输入端元素引索，j表示输出端元素的引索，k表示任意元素引索），注意与上面的那些大写字母加下标的意思不同，大写字母的下表标网络层次号。还有一个要注意的是就是，e^ok对oi的偏导只有当k=i时是非零值，其他时候都是0。
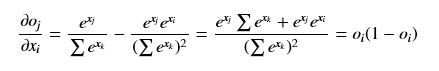(i == j)
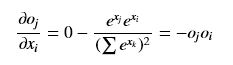(i != j)
- relu函数的导数(先用通用型的x来作为自变量)：
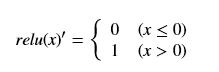
- 全连接层函数的导数就不用写了，就是一个简单的线性模型
推导权重的偏导
上面我们已经分析了对于两层多分类网络中，几个特定函数的导数或偏导，下面我将结合上面所有的知识，推导出其每个网络层次的导数，这里小写字母z、w、b第一层和第二层写法可能会重复，为了区分我加入上标表示不同网络层次，不是平方号。
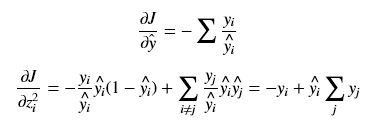
对于分类问题，Y中只有一个yi为1，其余的都为0，所以一般整合softmax cross entropy在一起，化简后其导数将变为非常简单的形式为：
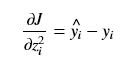
推导第二层的权重和偏置的偏导：
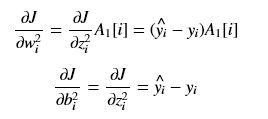
第一层的权重和和偏置的偏导计算类似，不过得先计算A1和Z1的偏导。
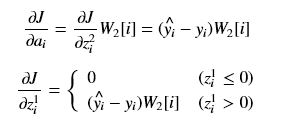
由于Z1的偏导是分段，为简化，为0的那段就不考虑了，因为它已经无法对前面的网络起作用了，所以下面只考虑不为0的那一部分，第一层的权重和和偏置的偏导:
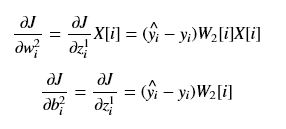
总结
初始化W和B后，根据前向的公式，我们可以逐层求出Z1、A1、Z2、Yhat、J；然后根据反向传播公式逐层反向求出各层的偏导。实际中，我们并不像上面一样需要写出偏导计算的最终公式，因为它只需要知道其上一层的偏导结果即可，但是得到最终的结果对于我们分析会有特别的好处。例如从上面的权重偏导公式中可以看到，其结果只与两个因素有关，一个是误差项，另一个就是其后面所有层次的权重成绩。
从这一点，我们可以很直接的看出，梯度爆炸与梯度消失的原因，正是由于浅层网络的权重偏导取决于后面所有网络权重的乘积，后面的W过大就会导致乘积项指数增大、而W过小又会导致其乘积越来越接近于0。当然梯度爆炸与梯度消失的主要原因是由于选用的不好的激活函数，我们这里使用的是relu，它在输入值大于0的时候，导数稳定为1所以，所以我们在公式的乘积中没有激活函数导数项，这样的激活函数不会随层次增加而衰减或爆炸。