前言
在了解过EM算法后,再来看GMM就轻松多了,当然对于我来说除了GMM的基本原理外,更重要的是需要利用GMM算法来做视频的运动检测。
GMM简介
GMM是Gaussian Mixed Model的简称,中文名为高斯混合模型,基本原理其实十分简单,就是用多个不同的高斯模型线性叠加来拟合实际的数据分布。如下图为截取网友介绍GMM博文的图像,其中使用了两个高斯分布来拟合的实际的数据点分布:
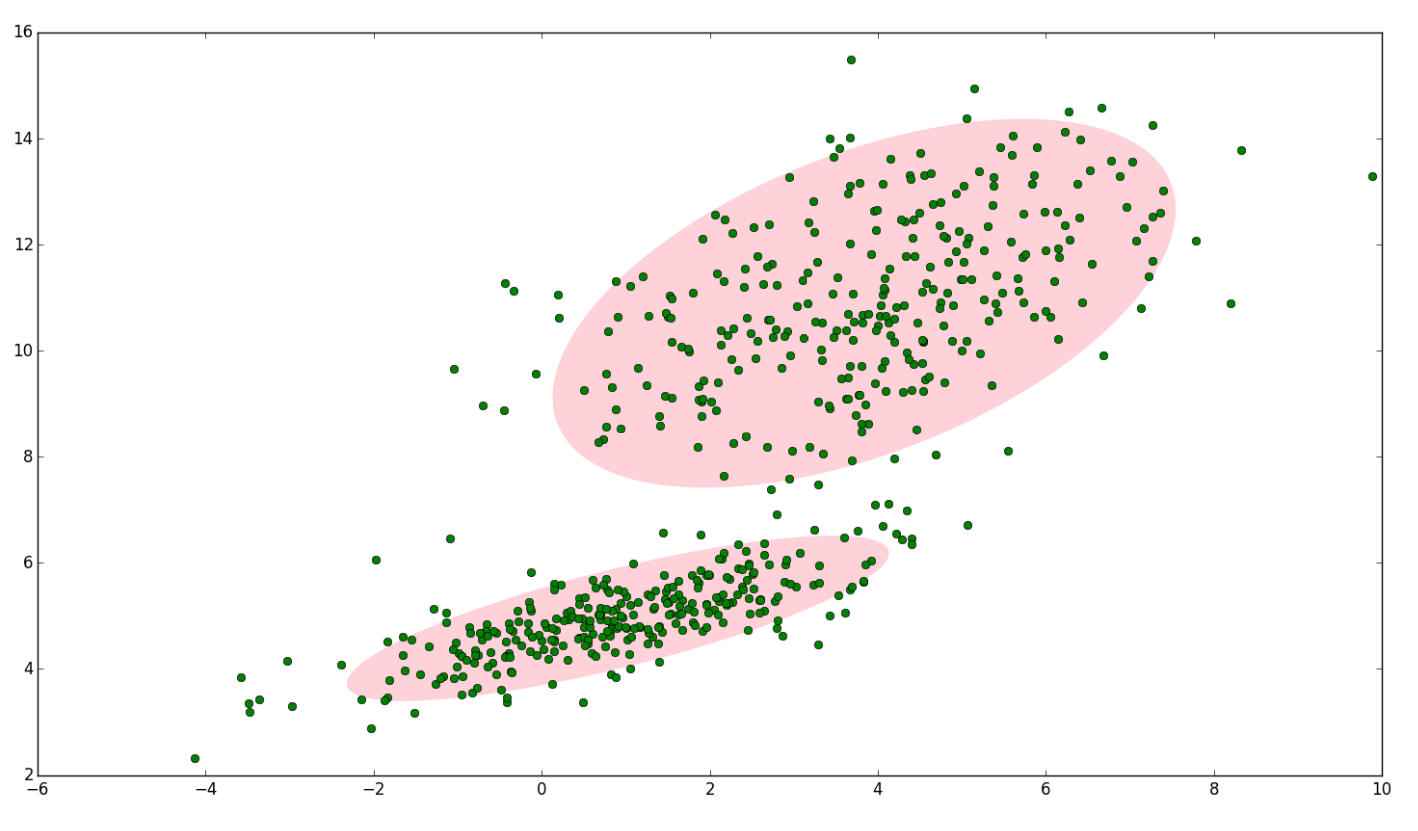
假定有随机变量x,混合高斯模型的公式表达形式为:
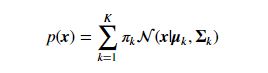
p(x)表示x发生的概率,它由K个不同的高斯分布组成,πk相当于每个分量的权重,详细说明可以看参考中第一篇博文的说明。
GMM和EM算法
虽然GMM的基本原理很简单,但是使用GMM要得到估计的最佳结果却不容易,对上图来说就就是两个高斯的均值、方差以及各自占的权重。为了计算得到GMM的最优的估计参数就需要使用到EM算法,所以理解GMM方法的难点实际上是需要理解EM算法在GMM中的使用,而实际上EM算法真是不是那么好理解。
对于EM算法我在上篇单独做了简要的说明,我们可以看到GMM这样的形式非常适合用EM算法来就解,因为EM算法来说就是为了解决由于隐变量的存在导致目标参数相互影响的问题的方法,在GMM中这个隐变量就是每个高斯分量的类型;另外GMM的每个分量的形式都是已知的,都是高斯分布,所以使用EM算法计算最大似然也是非常方便。
使用GMM做检测视频的运动检测
在视频处理中GMM是一种非常常用且有效的运动检测方法,它的主要作用是将场景中的前景和背景分离。它是对图像的每个像素建立多个高斯模型,每个模型包含均值、方差、权值和匹配数4个参数,我们可以看到,除了匹配数其他参数都是上面公式里包含了的。在GMM使用前需要设置好高斯模型的个数,这是需要人为指定的。然后根据第一帧图像初始化第一个高斯模型的参数,而其他的高斯模型则使用0初始化。
在后续帧输入时,使用当前图像的每个像素值对于其对应的高斯模型进行匹配,一种匹配的方法是:计算当前像素值与要匹配的高斯模型的偏离均值的大小,若小于阈值则匹配成功。完成匹配的操作后,使用新匹配的数据更新模型的参数,最后进行高斯模型排序,不过这个排序是根据权值方差来定的,具体可以看参考链接2。
图像的背景为每个像素的灰度值其对应的第一个高斯模型的平均值,当当前图像像素值与已存在的第k个高斯模型匹配,并且前k-1个高斯模型的权值之和小于阈值bg_threshold ,则将当前像素归为背景,像素值设为0,否则归为前景,像素值设为255。
在opencv中的使用
GMM在opencv中有对应的算法实现:BackgroundSubtractorMOG和BackgroundSubtractorMOG2,BackgroundSubtractorMOG2是在BackgroundSubtractorMOG的改进,具体可以查看opencv的文档。
opencv的官方文档中提供了简单的使用实例:
1 | import numpy as np |