蒙特卡洛算法简介

技术算法

2017-09-22

这两年随着AlphaGo等一大票围棋AI的崛起，隐藏在其背后蒙特卡洛算法也开始为大众所知，不过基本上大多都和我一样是只闻其名、不知其物。最近复习概率论，看到蒙特卡洛算法，感到很意外，没有想到威力强大的蒙特卡洛算法在原理上竟然是如此的简单。

蒙特卡洛，英文：Monte Carlo method，蒙特卡洛方法灵活多变，但核心都是使用随机数（或伪随机数）去了解一个系统，从而来解决很多计算问题的一类方法，所以很多文档中都说的是蒙特卡洛方法而不是算法。

从概念上看，这个说明是相当抽象的，一下通过实例来说明，会发现蒙特卡洛方法实际上可以非常简单。

这也许是在讲解蒙特卡洛方法时最常用的一个实例，在求π值的方法，我觉得这个方法也许是最简单的。

如何求解，我们在构造一个正方形和它的内切圆，如下图所示：

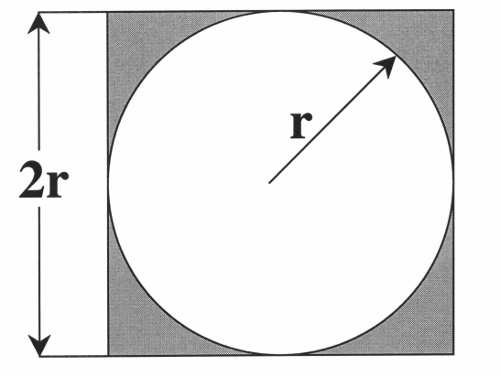
我们在正方形的面积内随机选择一个点，大量的重复该随机实现，统计点落在内切圆内的次数。从概率论的知识可以知道，这种重复独立实现的概率分布服从中几何分布，随机点在圆内的概率是正方形和内切圆的面积之比，因此就可以通过实现统计出来的结果近似的看成随机出现在圆内的概率，从而求出π值。

就是如此的简单粗暴，这种看似暴力的做法，不仅原理上很简单，而且通过计算机能够很方便的编程实现。通过在指定的空间域内产生随机数，统计验证系统的分布结果，近似的看成系统的分布概率，以此来求解，这就是蒙特卡洛方法。

利用蒙特卡洛方法可以求任意的定积分值。实际上求积分就是上面求π值方法的推广，一一元为例，定积分可以看成是函数曲线在和横轴的在积分域内的面积，通过构造包含该面积的一个长方形，然后使用随机数，统计在积分区域面积的概率，实际上就和上例一样了。