图像修复原理和大致流程
如下图所示,为从原始图像到被破坏再到被修复的整个流程的模型框图:
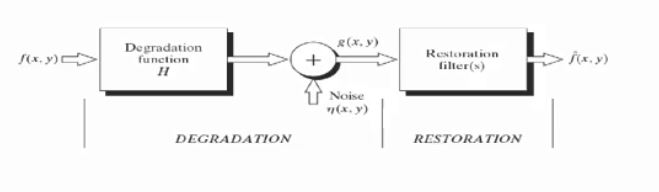
上图,原始图像f(x,y),经过退化函数H,然后又叠加入了噪声成为被破坏后的图像g(x,y),图像修复的目的找出对应的处理滤波器,尽量的还原原始图像f(x,y)。
原始图像退化的原因可能有:拍摄时没有对焦,运动产生的模糊。噪声加入的原因也能够使多方面的,有可能是拍摄设备本身的电磁噪声。因此从f(x,y)到g(x,y)可以写成如下表达式:
g(x, y) = f(x,y) * h(x, y) + n(x, y)
注意:1. f(x,y)与H(x,y)是卷积的操作 2. 噪声大多数都是加性噪声,如果有少量的乘性噪声,其处理方法也可以将其转换为家性噪声,然后以加性噪声的方法来处理
由于我知道了图像破坏的模型后,图像的修复就是其逆过程,我们如果可以知道了H(x,y)和n(x,y),就可以反推得到原始图像f(x,y)。
噪声模型
为了方便研究H(x,y)和n(x,y),研究者们总结出了一些常用的噪声模型,这些噪声模型既包含了理论的模型也含有实际出现的噪声,可以方便大家套用和简化计算。我这里只是简单介绍其特性,其函数表达式以及详细分析可以参考其他专业资料。
以下为6种常用的噪声模型的函数曲线图。
高斯噪声(Gaussian)
如上图所示第一条曲线为高斯噪声。高斯噪声是一种理想的模型,服从正太分布,在实际情况中不会出现,但是高斯噪声使用确实非常广泛的,其原因之一是数学上很好计算,其次它是其他噪声很好的近似。
瑞利噪声(Rayleigh)
上图中第二条曲线为瑞利噪声,是在实际中存在的噪声,比如磁共振。
伽马噪声
上图第三条曲线为伽马噪声。
指数噪声
上图第四条曲线为指数噪声,起一个重要的特征是没有负噪声。当图像做预测编码是导致的误差是指数噪声。
均匀噪声
上图第五条曲线为均匀噪声,当图像做量化时导致的量化噪声就是均匀噪声。
脉冲噪声
上图中的最后一条曲线为脉冲噪声,椒盐噪声就是属于脉冲噪声的类型。
这里有网友总结的各个噪声模型的表达式和Matlab代码可供参考:http://www.myexception.cn/image/1709093.html
图像噪声类型的评估
图像加入噪声后的图像的直方图分布会受到噪声的影响,直方图的分布会变得和其加入的噪声的分布类似,因此我们可以通过检测图像的直方图来评估噪声类型。
实际操作时,我们为了让直方图更明显,先取图像中颜色变化较小的一小块区域来做直方图,这样一来,直方图的形状就主要受其噪声类型的影响。但是如果整个图像噪声分布不是均匀的,那就可能要在不同位置多取几个区域检测了。
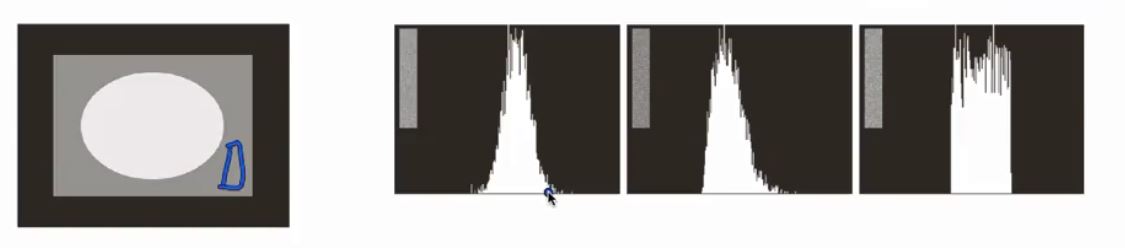
如上图,最坐标的原始图像,取蓝色框中的区域得到其直方图,因此可以很直接的看出:最左边的直方图是高斯噪声,中间是瑞利噪声,最右边的是均匀噪声。
另外,如果直方图从肉眼不能直观的区分噪声类型,那么可以通过一一猜测的办法,通过用标准的工具做函数拟合,看看那种类型拟合出来的误差小。
噪声的处理
从前面图像破坏的模型表达式可以看到,一般的噪声都是加性的噪声,而通过前面的噪声评估我们可以得到噪声的类型,图像修复是要去除噪声,就可以做逆向操作:
g(x, y) - n(x, y)
退化函数的评估
通常退化函数也被称为模糊函数,前面提过主要是两种情况:拍摄时没有对焦,运动产生的模糊。
评估退化函数比较困难,有时候会需要一些实验和尝试。一般拍摄失焦的情况与高斯模糊比较类似,可以用高斯模糊来模拟。运动运动模糊,则可以理解为运动图像在时间上的积分。
退化函数的处理
退化函数对原始图像是卷积的作用,图像修复为了去除退化函数的影响,通常的操作是利用傅里叶变换。
假定噪声已经去除,则原始图像被破坏的表达式为:
g(x, y) = f(x, y) * h(x, y)
对上式做傅里叶变换(注意下式的x是乘号):
G(u, v) = F(u, v) x H(u, v)
这样操作后表达式就从卷积运算变成了乘法操作,得到:
F(u, v) = G(u, v) / H(u, v)
最后再做傅里叶逆运算。