前言
承接上一篇求连通域的文章，本文继续复习整理关于图像处理和图像算法的一些基本知识点。
高斯模糊公式
高斯模糊，算是我们接触图像处理后最最基本的功能了，但是到现在我也没法写出高斯模糊的数学公式和标准高斯分布下高斯核模板取值情况，所以这里特地将其提取出来复习。
1. 一维高斯函数
在开始前，我先复习以下一维连续情况下的高斯函数的一般形式：
$$ f(x) = a e^{-\frac{(x-b)^2}{2c^2}} $$
而高斯分布的概率密度，则增加了函数在整个定义域内积分为1的约束，所以就成了我们习惯看到的形式（推导就不写了），mu为均值，sigma为标准差：
$$ f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$
2. 二维高斯分布函数
由于图像是二维的数据，所以应用于图像的高斯分布函数也是二维的。一般的二维的高斯函数可以看成两个一维的高斯函数的乘积，形式如下：
$$ f(x,y) = a e^{-\frac{(x-\mu_x)^2}{2\sigma^2_x}-\frac{(y-\mu_y)^2}{2\sigma^2_y}} $$
通常在图像领域x、y属于统一分布，且x、y为坐标，其均值为其中心坐标，一般设置为0，因此就得到了图像中的二维高斯分布的连续的密度函数为：
$$ f(x,y) = \frac{1}{2\pi \sigma^2} e^{-\frac{x^2 + y^2}{2\sigma^2}} $$
3. 高斯核
首先数字图像是离散的，所以需要将上面的连续函数改为离散的形式，其次图像的尺寸是由大小，所以图像中的离散的高斯分布函数通常定义域只是一个小的区域。在实际使用中我们一般取一个n x n的矩形小区域，一般将n设为奇数保证它的中心坐标是一个整数，且坐标正负对称。
因此，我们可以将n x n矩形范围内的每一个坐标上（像素点）的高斯分布函数的值直接求出来，这就是高斯核。使用高斯核，可以减少重复的计算。在高斯模糊的实现中，就是使用高斯核作为每个坐标位置的权重来做平均。
假定标准差为1.5的一个3x3的高斯核模板如下：
sobel算子
sobel算子可用于计算图像的梯度在前面的梯度的文章就介绍过，但是并没有写出典型的模板值。为什么使用sobel算子来计算图像的梯度，
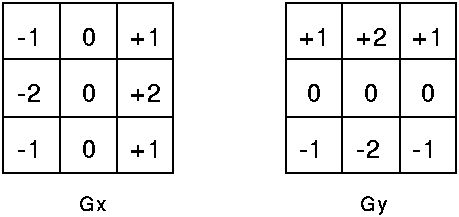
另外这里需要提示的是，由于sobel经常用于边沿检测，所以有时候我说检测边沿方向，而不是说梯度方向，这两者说法是不一样的，从广义上来将可以认为这两说法刚好是反的，所以刚刚接触到的时候后，常常会不注意看错或混淆这两个说法。计算水平方向（x）的梯度，作用等同检测垂直方向的边沿；而计算垂直方向上（y）的梯度，作用等同于检测垂直方向上的边沿。如下为典型的3x3的两个梯度方向的sobel模板：
拉普拉斯算子
1. 拉普拉斯算子的数学公式
在图像处理中，常将laplace（拉普拉斯）算子和sobel算子一起说明，主要是因为它们都是图像的微分算子，都可以用于边沿检测，两者的本质区别在于，sobel是一阶微分，而laplace则是二阶微分，对于连续二维函数其拉普拉斯算子定义为：
$$ Laplace(f) = \frac{\partial^2{f}}{\partial x^2} +
\frac{\partial^2{f}}{\partial y^2} $$
拉普拉斯算子定义的是梯度的散度，推导后是各个维度的二阶导数的相加，它和sobel算子不一样，它在不同方向上的值是一样，因此它具有旋转不变性。
对于离散的图像，使用基本的前后差分求梯度，有：
$$ \frac{\partial^2{f}}{\partial x^2} = [f(x+1,y) - f(x,y)] - [f(x,y) -
f(x-1,y)] = f(x+1,y)+f(x-1,y)-2f(x,y)$$
$$ \frac{\partial^2{f}}{\partial y^2} = [f(x,y+1) - f(x,y)] - [f(x,y) -
f(x,y-1)] = f(x,y+1)+f(x,y-1)-2f(x,y)$$
计算公式将变成：
$$ \nabla f(x, y) = f(x+1,y) + f(x-1,y) + f(x,y+1)+ f(x,y-1) -4f(x,y) $$
2. 拉普拉斯算子模板
一般我使用如下两种3x3的权重数据作为拉普拉斯算子的模板（前一种就是按照上面的离散定义，第二种是扩展后的）：
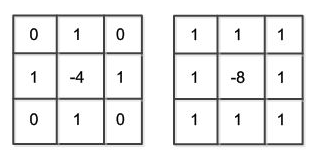
拉普拉斯算子对孤立点或端点更为敏感，因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合，对于一阶梯度是看幅值，而拉普拉斯算子则看零点。
另外使用拉普拉斯算子可以对图像进行锐化处理，使灰度反差增强，从而使模糊图像变得更加清晰。基本的锐化操作为：对图像进行拉普拉斯算子处理，将生成的图像与原始图像叠加，即可得到更加锐化的图像（这种简单的办法缺点是对图像中的某些边缘产生双重响应）。
高斯拉普拉斯算子
1. LoG的数学公式
高斯拉普拉斯算子(Laplacian-of-Gaussian)简称LoG，是高斯和拉普拉斯的双结合，实际上就是由于拉普拉斯算子抗噪声能力太弱，所以就在前面加入高斯滤波后再做拉普拉斯计算。
公式上就是对二维高斯分布公式进行拉普拉斯算子处理，两次求导后结果如下：
$$ LoG = \frac{x^2 + y^2 - 2\sigma^2}{\sigma^4} e^{-\frac{x^2+y^2}{2\sigma^2}}$$
一个比较小的典型LoG模板如下：
2. 高斯差分算子
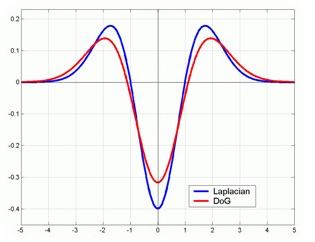
由于计算LoG比较复杂，所以在实际中为了减少计算量，通常使用高斯差分算子(DoG,Difference of Gaussian)来近似，DoG的是两个同均值不同方差的高斯分布相减的结果，在结果上与LoG非常的相似。
使用g表示一个高斯分布函数，则DoG公式为：
$$ DoG = \frac{g(x, y, k\sigma)-g(x,y,\sigma)}{k\sigma-\sigma}$$
DoG与LoG的对比图：
参考
- 高斯函数（Gaussian function）的详细分析
- 差分近似图像导数算子之Laplace算子
- 图像边缘检测——二阶微分算子（上）Laplace算子、LOG算子、DOG算子（Matlab实现）
- LOG高斯-拉普拉斯算子
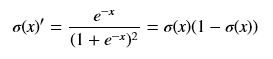
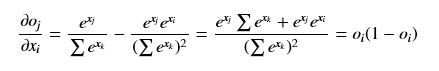(i == j)
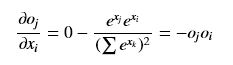(i != j)
